Module 3: Patterning

 

 

Observing and creating patterns creates a richer and deeper understanding of the world because it pushes us to recognize meaning in what may otherwise be considered chaos.  I focused on two patterns in my theme of graphing in algebra.  One was the pattern of change when altering the “b” value in a linear equation of the form y = mx +b and the other was the pattern of change when altering the magnitude of the “a” value in quadratic equations of the form y = ax2.  As the b value changes in a linear equation we discover the resulting lines shift vertically.  Making this change by equivalent intervals reveals a pattern of parallel lines.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

If we inverse the value of the slope in the linear equation as well and graph the same changes in the “b” values, these two overlaid patterns create a new latticework pattern.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

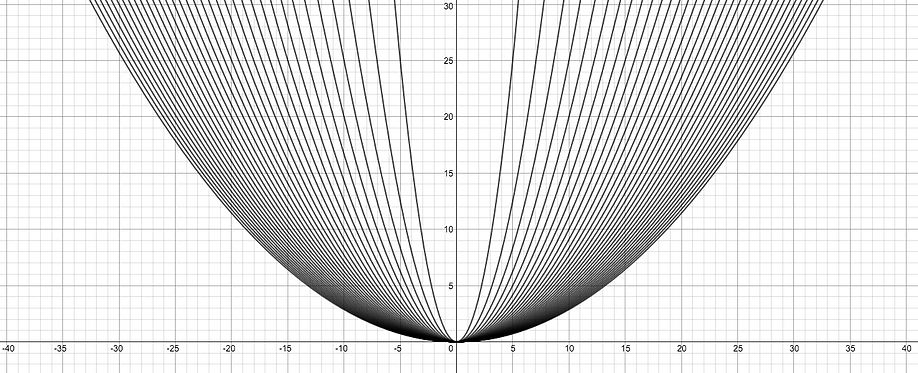
Shifting to the quadratic equation, as the “a” value decreases and approaches 0 the pattern of change can be observed in the resulting graphs that the parabola grows wider and wider.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

If we invert the sign of the “a” value we see a similar pattern but the parabolas open down rather than up due to the negative sign.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

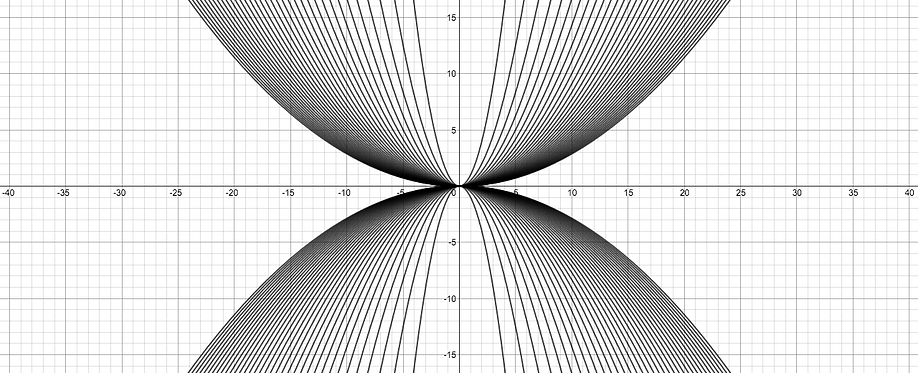
These are normal, observed patterns in algebra, and although interesting in nature, they do not result in any sort of novel pattern.  However, if we try something new and overlay the latticework linear patterns with the widening parabolas, we create a new and beautiful juxtaposition between linear and parabolic graphs which also includes touches of moiré like patterning.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

With this new overlay, the differences between the straight lines of linear equations and curved parabolas of quadratic equations become more pronounced and observable.  For example, the linear patterns when we invert the slope creates an overlapping perpendicular pattern, but when we invert the coefficient of the squared x in the quadratic equations the resulting parabolas do not intersect apart from at the origin of the graph.  This juxtaposition creates a richer understanding of how changes in linear equations have different results than changes in the quadratic equations.

 

If observing closely the changes in the linear equations (which are available for viewing here), perhaps one may be astute enough to notice when changing the b value of the linear equations I was changing a constant whereas when changing the a values of the quadratic equations I was changing a coefficient.  This hopefully creates an interest in the question of what will happen if I change the c value in the expanded quadratic equation of y = ax2 + bx + c. 

 

Observing what is changing in the graphs as the equations are altered is an important part of developing the deeper and richer understanding, however we must not ignore the contrasting observation of what is not changing as we alter the equations.  This line of questioning also develops a deeper and richer understanding of the graphs.  This is akin to helping students develop the perception of nothingness as yet another tool with which to perceive algebra.